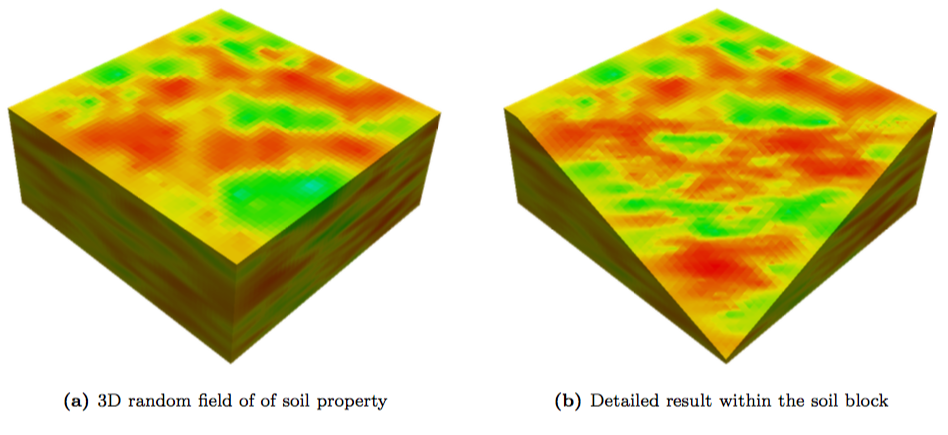
Spatial structure in inhomogeneous geomaterials
Many studies about liquefaction found in literature were based on two-dimensional analyses of soil liquefaction (in a vertical plane) assuming plane strain behavior. Therefore the correlation distance of soil variability in a direction normal to the plane of analysis was implicitly taken as infinite (i.e. no variability in the third direction).
An attempt to address the real 3D aspect of the problem was presented by [1] with an analysis of liquefaction potential at the Wildlife Site, Imperial Valley, California. The soil properties were modelled as a 3D random field; however, the liquefaction analysis was carried out in 1D vertical columns, without any coupling in the horizontal plane. Consequently, the study could only address the pointwise initiation of liquefaction, and did not include the effects of pore water pressure redistribution before and after initial liquefaction. Through this 3D approach, the authors provided interesting observations on the clustering of liquefied zones in a horizontal plane.
Another stochastic analysis of the same site was presented by [2]. The soil properties and the probabilistic characteristics of their variability were estimated based on a limited number of cone penetration test(CPT) results. A 3D stochastic analysis was performed, but the liquefaction potential was assessed separately at each point in space using an empirical method (e.g. [3]; [4]). Though this approach could not capture any interaction between zones of soil with different liquefaction strengths and different amounts of pore water pressure build-up, the study provided some interesting conclusions on the effects of loose soil zones on the probability of liquefaction failure.
Liquefaction and many other geotechnical engineering problems are multiscale in nature because of inho- mogeneities existing at different length-scales in geomaterials. None of the investigations mentioned previously has addresses the multiscale issue of 3D modeling of liquefaction in inhomogeneous geomaterials. We initiated a project on the evaluation of liquefaction resistance of soil considering its 3D inhomogeneity.
[1] G. A. Fenton and E. H. Vanmarcke. Spatial variation in liquefaction risk. Geotechnique, 48(6):819–831, 1998.
[2] T. Elkateb, R. Chalaturnyk, and P. K. Robertson. Simplified geostatistical analysis of earthquake- induced ground response at the Wildlife Site, California, USA. Canadian Geotechnical Journal, 40(1): 16–35, 2003.
[3] H. B. Seed and I. M. Idriss. Simplified procedure for evaluating soil liquefaction potential. Journal of the Soil Mechanics and Foundations Division, 1971.
[4] P. K. Robertson and C. E. Wride. Evaluating cyclic liquefaction potential using the cone penetration test. Canadian Geotechnical Journal, 35(3):442–459, 1998.
···